Vydáno:
Pokud máme zadáno n kontrolních bodů, nemůžeme křivku interpolovat polynomem nižšího, než n-1 stupně (za předpokladu, že na dané křivce nižšího stupně neleží všechny body). Takovou křivku můžeme však aproximovat křivkou nižšího stupně. Například metodou nejmenších čtverců. Toto řešení se snaží minimalizovat součet čtverců odchylek oproti původní křivce.
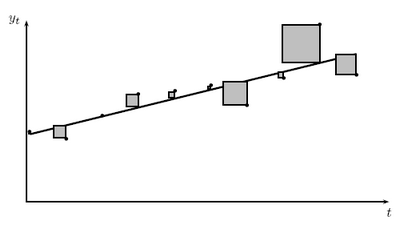
Zdroj obrázku: http://www.eistat.cz/
Mějme zadáno 5 bodů:
$$
P_1 = [1,1], P_2 = [3,2], P_3 = [5,4], P_4 = [6,3], P_5 = [7,2]
$$
které chceme aproximovat polynomem 3 stupně:
$$
y = a_0x^3+a_1x^2+a_2x+a_3
$$
Po dosazení bodů do rovnice získáme 5 rovnic o 4 neznámých. Taková rovnice nemá řešení.
\begin{align*}
1 = {}&a_0+a_1+a_2+a_3\\
2 = {}&27a_0+9a_1+3a_2+a_3\\
4 = {}&125a_0+25a_1+5a_2+a_3\\
3 = {}&216a_0+36a_1+6a_2+a_3\\
2 = {}&329a_0+49a_1+2a_2+a_3\\
\end{align*}
Vytvoříme proto reziduální funkci ve tvaru:
\begin{align*}
f = {}&(a_0+a_1+a_2+a_3)^2+(27a_0+9a_1+3a_2+a_3)^2+(125a_0+25a_1+5a_2+a_3)^2\\&+(216a_0+36a_1+6a_2+a_3)^2+(329a_0+49a_1+2a_2+a_3)^2
\end{align*}
Parciální derivaci funkce $f$ podle $a_0,a_1,a_2,a_3$ získáme tyto 4 rovnice:
\begin{align*}
f_{a_0} = {}&2(a_0+a_1+a_2+a_3)+54(27a_0+9a_1+3a_2+a_3)+250(125a_0+25a_1+5a_2+a_3)\\&+432(216a_0+36a_1+6a_2+a_3)+658(329a_0+49a_1+2a_2+a_3)
\end{align*}
\begin{align*}
f_{a_1} = {}&2(a_0+a_1+a_2+a_3)+18(27a_0+9a_1+3a_2+a_3)+50(125a_0+25a_1+5a_2+a_3)\\&+72(216a_0+36a_1+6a_2+a_3)+98(329a_0+49a_1+2a_2+a_3)
\end{align*}
\begin{align*}
f_{a_2} = {}&2(a_0+a_1+a_2+a_3)+6(27a_0+9a_1+3a_2+a_3)+10(125a_0+25a_1+5a_2+a_3)\\&+12(216a_0+36a_1+6a_2+a_3)+4(329a_0+49a_1+2a_2+a_3)
\end{align*}
\begin{align*}
f_{a_3} = {}&2(a_0+a_1+a_2+a_3)+2(27a_0+9a_1+3a_2+a_3)+2(125a_0+25a_1+5a_2+a_3)\\&+2(216a_0+36a_1+6a_2+a_3)+2(329a_0+49a_1+2a_2+a_3)
\end{align*}
Každou z rovnic položíme nule a spočítáme jednotlivé koeficienty $a_0, a_1, a_2, a_3$. Jednotlivé koeficienty, resp. jejich výpočet, můžeme zapsat a spočítat pomocí maticového zápisu.
$$
{\begin{bmatrix}
\sum\limits_{i=1}^n x_i^{2k} & \ldots & \sum\limits_{i=1}^n x_i^{k+1} & \sum\limits_{i=1}^n x_i^{k} \\
\vdots &\vdots &\vdots &\vdots \\
\sum\limits_{i=1}^n x_i^{k+1} & \ldots & \sum\limits_{i=1}^n x_i^{2} & \sum\limits_{i=1}^n x_i \\
\sum\limits_{i=1}^n x_i^{k} & \ldots & \sum\limits_{i=1}^n x_i & n \\
\end{bmatrix}
}
{\begin{bmatrix}
a_0\\
a_1 \\
\vdots \\
a_k \\
\end{bmatrix}
}
=
{\begin{bmatrix}
\sum\limits_{i=1}^n y_ix_i^k \\
\vdots \\
\sum\limits_{i=1}^n y_ix_i \\
\sum\limits_{i=1}^n y_i \\
\end{bmatrix}
}
$$
Tudíž podle námi zadaných kontrolních bodů získáváme matici:
$$
{\begin{bmatrix}
180660 & 27952 & 4404 & 712 \\
27952 & 4404 & 712 & 120 \\
4404 & 712 & 120 & 22 \\
712 & 120 & 22 & 4
\end{bmatrix}
}
{\begin{bmatrix}
a_0\\
a_1 \\
\vdots \\
a_k \\
\end{bmatrix}
}
=
{\begin{bmatrix}
1889 \\
325 \\
59 \\
12
\end{bmatrix}
}
$$
Pro výpočet můžeme zvolit některou z eliminačních metod a získáme koeficienty:
\begin{align*}
a_0 ={}& \frac{-2627}{72820} \approx -0.0356\\
a_1 ={}& \frac{15657}{72820} \approx 0.215\\
a_2 ={}& \frac{10482}{18205} \approx 0.576\\
a_3 ={}& \frac{-3562}{18205} \approx -0.196\\
\end{align*}
Po dosazení do rovnice, získáváme:
$$
f(x) = -0.0356x^3+0.215x^2+0.576x-0.196
$$
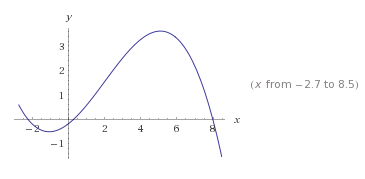
Výsledná aproximační křivka na intervalu -2.7 až 8.5
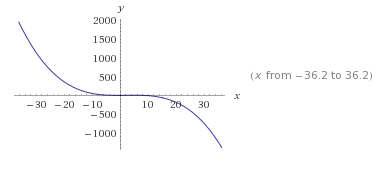
Výsledná aproximační křivka na intervalu -36.2 až 36.2