Derivace

Derivace je jeden ze základních pojmů diferenciálního počtu a můj oblíbený matematický aparát. Díky ní můžeme vyšetřit průběh funkce a na základě této znalosti například určit v jakém úhlu leží tečna v daném bodě, jak rychle se v daném bodě funkce mění nebo kde je její nejnižší či nejvyšší bod. A k čemu jsou tyto znalosti dobré v každodenním životě? Představme si, že chceme vytvořit počítačovou hru a máme funkci, která nám představuje dráhu autíčka na mapě. Tato funkce má tvar:

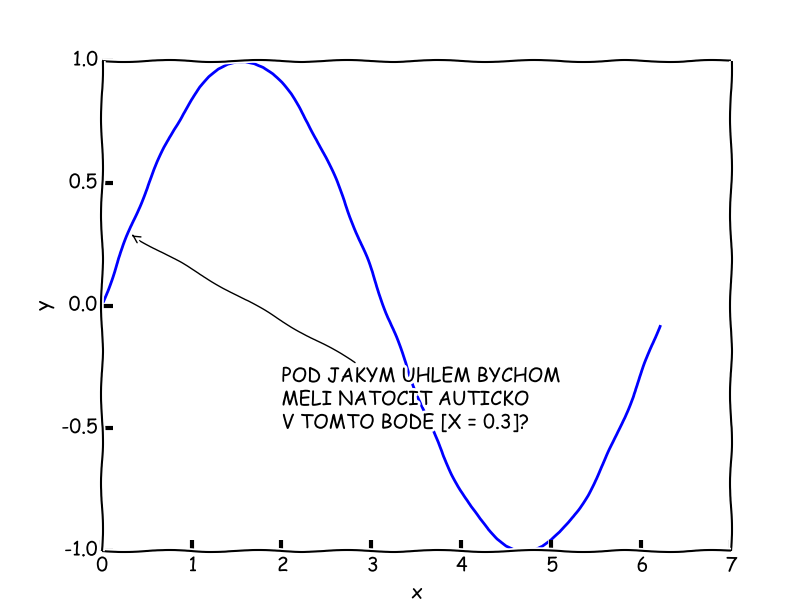
Derivace nám poskytuje prostředek, pomocí kterého zjistíme, jak máme naše autíčko v každém jednom bodě natočit. Trošku jiný příklad, tentokrát z počítačové grafiky a zpracování obrazu, může být detekce hran na fotografii.

Při zpracování obrazu se nám často hodí v takovémto obrázku zvýraznit hrany (vytvořit jakýsi obrys), najít místa, kde je velká změna jasu. Díky znalosti hran můžeme obrázek segmentovat (najít zájmové oblasti/objekty) či triviálně klasifikovat (rozhodnout, čeho je to obrázek). Jelikož se v počítačovém zpracování nejčastěji setkáváme s diskrétním obrazem (takový, který se skládá z pixelů) a ne obrazem spojitým, který bychom získali pomocí spojité obrazové funkce, provádíme nad obrazem diskrétní derivaci - diferenci.

A jak to vlastně funguje?

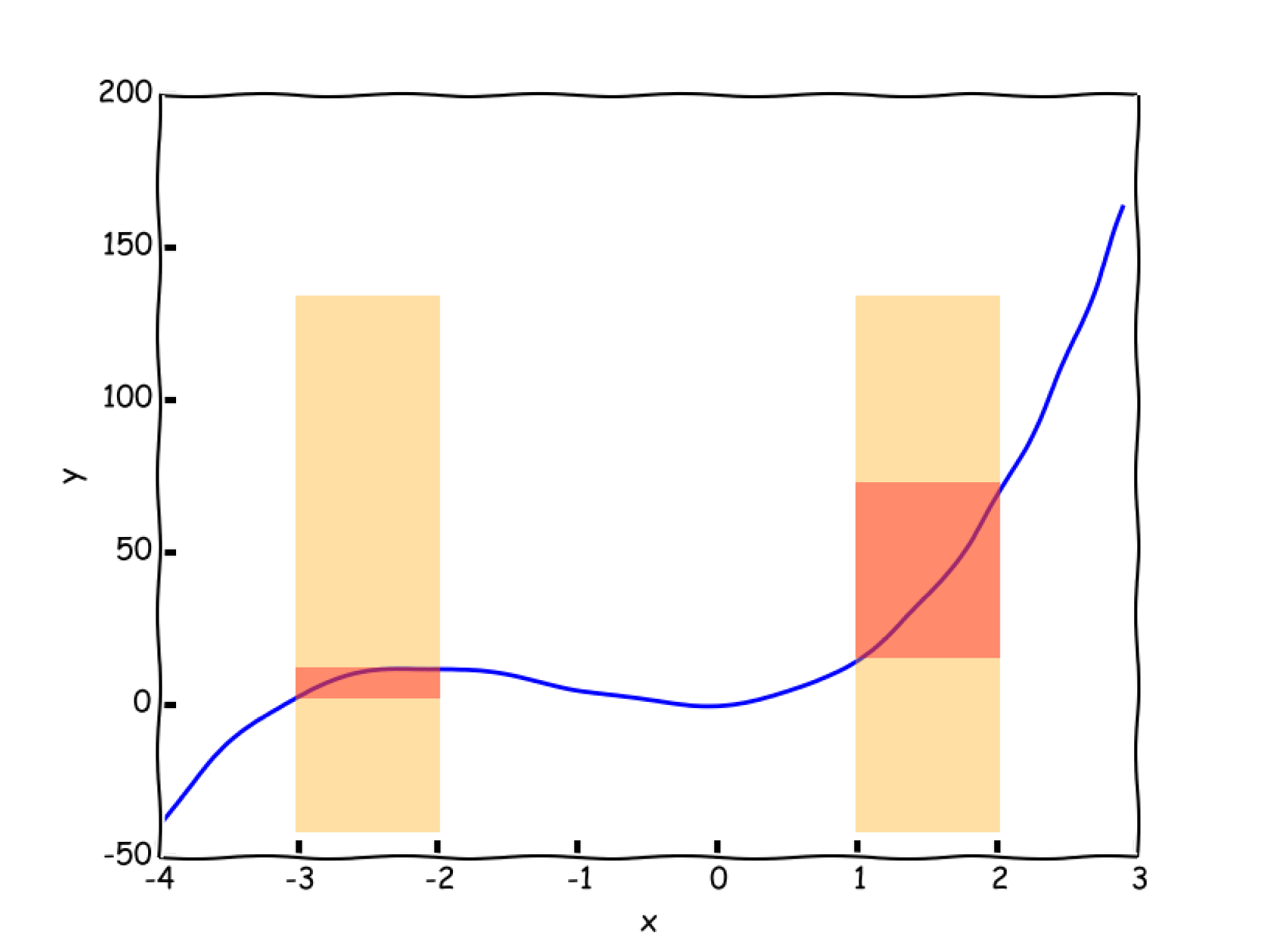
Představme si, že máme níže popsanou funkci. Zajímá nás, jak moc funkce rostla nebo klesala na nějakém intervalu. Máme interval $\langle-3;-2\rangle$ a $\langle1;2\rangle$. Už pouhým pohledem vidíme, že funkce na prvním intervalu roste podstatně pomaleji, než na intervalu druhém. Nyní si představme, že budeme interval zmenšovat a zjišťovat tak, jakou má funkce odezvu na co nejmenší změnu parametru – a to je vlastně hodně zjednodušená definice derivace. (Derivace nějaké funkce je změna (růst či pokles) obrazu této funkce v poměru k (ideálně) nekonečně malé změně jejích argumentů)

Většinou derivujeme za pomocí znalosti derivace elementárních funkcí, což jsou takové ty tabulkové (jako že derivace $f'(3x) = 3$ atd.), které nám pomáhají urychlit a zjednodušit výpočet. Ve skutečnosti je derivace limitou, jak jsem se snažil naznačit výše. Taková limita má tvar:

$$ f'(x) = \lim_{h\to0} {\frac{f(x+h)-f(x)}{h}} $$

Na této limitě vidíme přesně to, o co se snažíme. Hledáme derivaci v nějakém bodě $x$. Od tohoto bodu se posuneme nekonečně malý kousek $h$ (tudíž $h$ se blíží 0). Rozdíl nám potom dá odezvu funkce právě na intervalu nekonečně malé délky $h$. Pravdivost tvrzení, že derivace je limita si zkusíme ověřit. Nejdříve zderivujeme funkci pomocí pravidel pro derivaci elementárních funkcí a zjistíme tak hodnotu derivace v bodě $x = 1$

\begin{align*} f(x) &= 3x^3+10x^2+2x\\ f'(x) &= 9x^2+20x+2\\ f'(1) &= 9+20+2\\ f'(1) &= 31 \end{align*}

Derivace této funkce v bodě $x = 1$ nám vyšla 31. Zkusíme nyní derivaci vypočítat pomocí limity:

\begin{align*} f'(x) &= \lim_{h\to0} {\frac{f(x+h)-f(x)}{h}}\\ f'(x) &= \lim_{h\to0} {\frac{(3(x+h)^3+10(x+h)^2+2(x+h))-(3x^3+10x^2+2x)}{h}}\\ f'(x) &= \lim_{h\to0} {\frac{(3(x^3+3x^2h+3xh^2+h^3)+10(x^2+2xh+h^2)+2x+2h)-(3x^3+10x^2+2x)}{h}}\\ f'(x) &= \lim_{h\to0} {\frac{3x^3+9x^2h+9xh^2+3x^3+10x^2+20xh+10h^2+2x+2h-3x^3-10x^2-2x}{h}}\\ f'(x) &= \lim_{h\to0} {\frac{9x^2h+9xh^2+3h^3+20xh+10h^2+2h}{h}}\\ f'(x) &= \lim_{h\to0} {\frac{h(9x^2+9xh+3h^2+20x+10h+2)}{h}}\\ f'(x) &= \lim_{h\to0} {9x^2+20x+2}\\ f'(1) &= 9x^2+20x+2\\ f'(1) &= 31\\ \end{align*}

Jak jde vidět, výpočet pomocí limity se shoduje s výpočtem pomocí derivací parciálních funkcí. Jenom jsme si trošku více započítali. Co však znamená výsledné číslo 31?

Co znamená výsledek derivace v bodě?

Výsledek derivace v nějakém bodě nám dává velikost směrnice tečny v tomto bodě. Směrnice je tangens úhlu, pod kterým přímka svírá osu $x$. Tady už se pomalu dostáváme k řešení úvodního příkladu s natočením autíčka. Že je to zatím moc komplikované? Pokusím se výše uvedené krok za krokem vysvětlit. Mějme následující rovnice přímky ve směrnicovém tvaru:

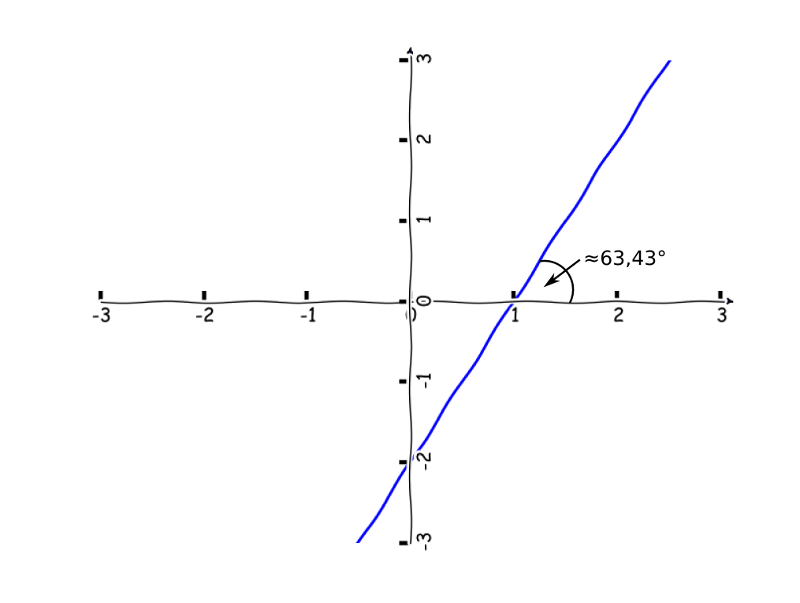
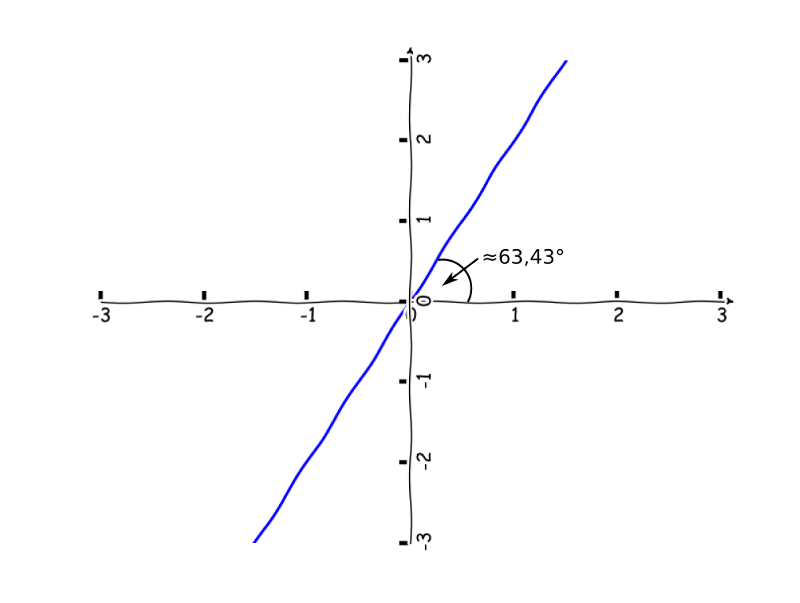
I když jsou obě přímky mezi sebou posunuty na ose x, mají stejnou směrnici. Směrnice je právě úhel, který svírají mezi osou $x$ a ten zůstává nehledě na posunutí stejný. A jak můžu vědět, že tento úhel je přibližně 63°? Když si vzpomeneme na goniometrickou funkci tangens, která nám říká, že tangens v pravoúhlém trojúhelníku je definován jako poměr protilehlé odvěsny k přilehlé, tak snadno. Řekněme, že si v druhém obrázku vyznačíme trojúhelník, který má délku jedné odvěsny na ose x = 1, na ose y = 2x

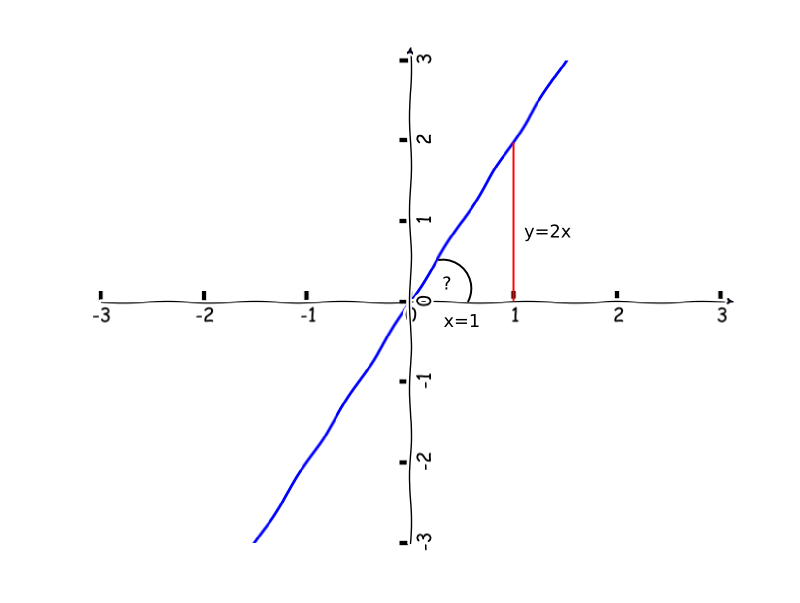
Potom dostaneme výpočet úhlu snadno takto:

\begin{align*} tan(\alpha) &= y/x\\ tan(\alpha) &= 2\\ \alpha &= arctan(2)\\ \alpha &\approx 63,43° \end{align*}

Malý postřeh - pokud máme přímku zadanou ve směrnicovém tvaru, tj. $y = kx + c$, tak koeficient $k$ je přímo směrnice, tj. tangens daného úhlu :-). Představme si nyní, že máme nějakou funkci, která nám představuje dráhu našeho autíčka. Autíčku budeme měnit pozici na ose $x$ na daném intervalu. Pozici na ose $y$ vypočítáme podle definovaného předpisu.

\begin{align*} f(x)=\frac{1}{3}x^2+2x\\ f'(x)=\frac{2}{3}x+2\\ f'(0)=2\\ \end{align*}

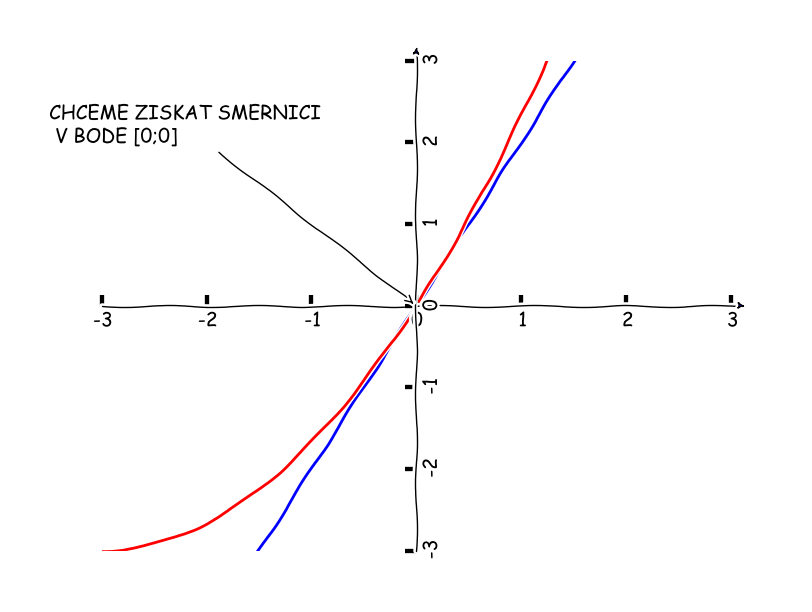
Nyní víme, že derivace naší funkce v bodě 0 je rovna 2. To nám dává směrnici - tangens úhlu který nás zajímá. Funkcí $arctan(2)$ získáme patřičný úhel a o ten naše autíčko natočíme. Co se směrnicí můžeme udělat dál? Můžeme zjistit tečnu - resp. rovnici tečny. Tečna je přímka, která se funkce funkce dotýká pouze v jednom bodě. Jistě by každý z nás uměl pro kvadratickou křivku (parabolu) najít libovolnou sečnu - přímku, která se křivky dotýká ve dvou bodech bodech. Aby limit nebylo málo, tak tečna je právě limitní případ sečny. V odstavci výše jsem zmínil směrnicový tvar přímky - v tomto tvaru můžeme zapsat libovolnou přímku a aktuálně se výhodně hodí pro zápis tečny. Obecná rovnice tečny má tento tvar:

$$ y-y_0 = f'(x)(x-x_0) $$

Hodnotu $f'(x)$ máme vypočítanou, hodnota $x_0$ a $y_0$ jsou souřadnice libovolného bodu, které na přímce leží. My aktuálně známe právě jeden bod, který na této přímce leží - bod dotyku s křivkou. Tj. $[0,0]$. Po dosazení získáme rovnici:

\begin{align*} y-0 &= 2(x-0)\\ y &= 2x \end{align*}

Proč se dají najít minima a maxima pomocí derivace funkce?

Nyní si hodně zjednodušeně představte, že směrnice je právě podíl změny hodnoty funkce na ose $y$ ku ose $x$ tj. $\frac{\Delta{y}}{\Delta{x}}$. Na následující funkci se budeme přibližovat k bodu, který bude představovat lokální maximum z levé a pravé strany. Čím víc se budeme k bodu přibližovat, tím se nám podíl tohoto rozdílu bude snižovat a blížit k nule. Až se dostaneme právě do bodu představující lokální maximum, bude podíl těchto hodnot právě nula. Pro ty z vás, co máte bujnou představivost, si můžete představit trojúhelník o nulové výšce a libovolné délce - takový trojúhelník bude sice vypadat spíše jako přímka, než cokoliv jiného, ale pro představu dejme tomu. Tangens úhlu mezi dvěma odvěsnami se bude rovnat samozřejmě nule. Takže teď víme, že hledáme ve funkci takové místa, kde se směrnice tečny rovnají nule. Kde se derivace této funkce rovná nule.

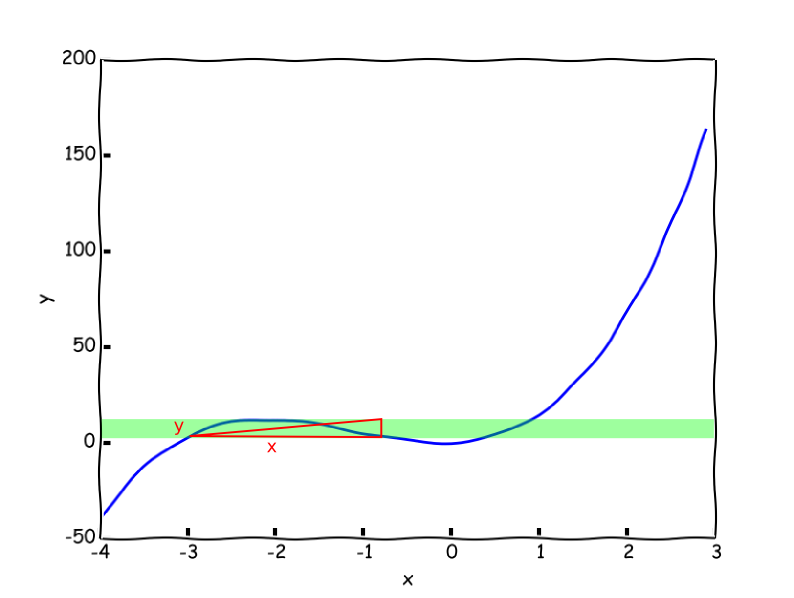
A jak se zjistí, které je minimum a které je maximum

Pokud libovolnou funkci zderivujeme, získáme funkci novou, o stupeň nižší. A tuto novou funkci můžeme analyzovat úplně stejným způsobem jako funkci původní a zjistit tak například znovu hodnotu směrnice v nějakém bodě. A právě toho využijeme při odhalení, zda se jedná o lokální minimum nebo maximum. Jako příklad si opět vezměme funkci $f(x)=3x^3+10x^2+2x$:

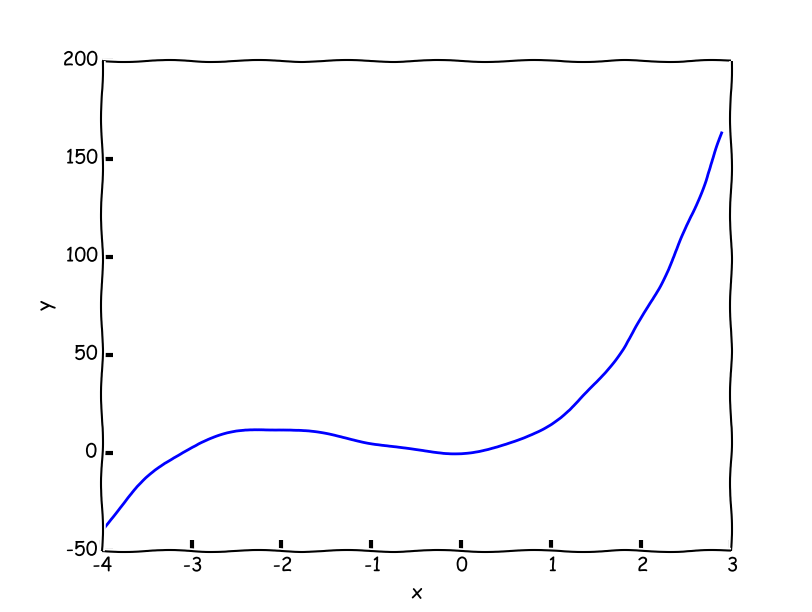
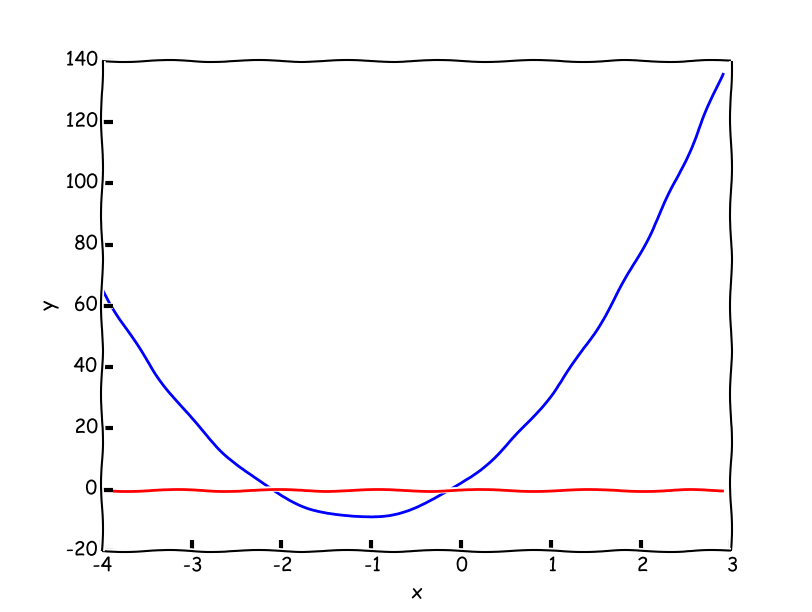
V grafu funkce první derivace vidíme zřetelně dvě místa, kde funkce prochází nulou. To jsou právě místa lokálních extrémů - stacionární body. Nyní se chvíli zamysleme a zkusme v těchto bodech odhadnout tečnu. Když se podíváme na graf původní funkce, v místě, kde odhadujeme lokální maximum, má tečna zápornou směrnici (když si představíme tečnu, tak pomyslně klesá). V místě možného lokálního minima má směrnice kladnou hodnotu (přímka pomyslně roste). V tomto okamžiku nám jde tudíž o to, abychom určili směrnici v těchto bodech z funkce první derivace. A to už umíme - funkci opět zderivujeme a ve stacionárních bodech určíme, zda $f''(x)>0$ pro lokální minimum nebo $f''(x)<0$ pro lokální maximum.

K čemu je dobrá znalost lokálních extrémů?

Ve výpočetní informatice se nám často hodí nějakou veličinu minimalizovat nebo maximalizovat - minimalizujeme nejčastěji chybu, jejíž velikost definujeme rovnicí, minimalizujeme pravděpodobnost špatné klasifikace obrázku do dané třídy, maximalizujeme výkon motoru apod. Ale o tom zase někdy příště...