Vydáno:
Perceptron je nejjednodušším modelem neuronových sítí. V tomto článku budu psát pouze o nejjednodušší variantě této sítě - jednom perceptronu, který pracuje s aktivační funkcí $\text{sgn}$ (signum, skoková funkce, hardlim, heaviside).
Jeden perceptron je schopen klasifikovat data (prvky nějaké množiny) do dvou tříd. Tyto data však musí být lineárně separovatelná - pokud máme prvky množiny ve 2D prostoru (máme 2 vstupní proměnné), tuto množinu jsme schopni rozdělit přímkou. Pokud jsme ve 3D prostoru (3 vstupní proměnné), budeme prostor dělit na dvě disjunktní oblasti dělící rovinou.
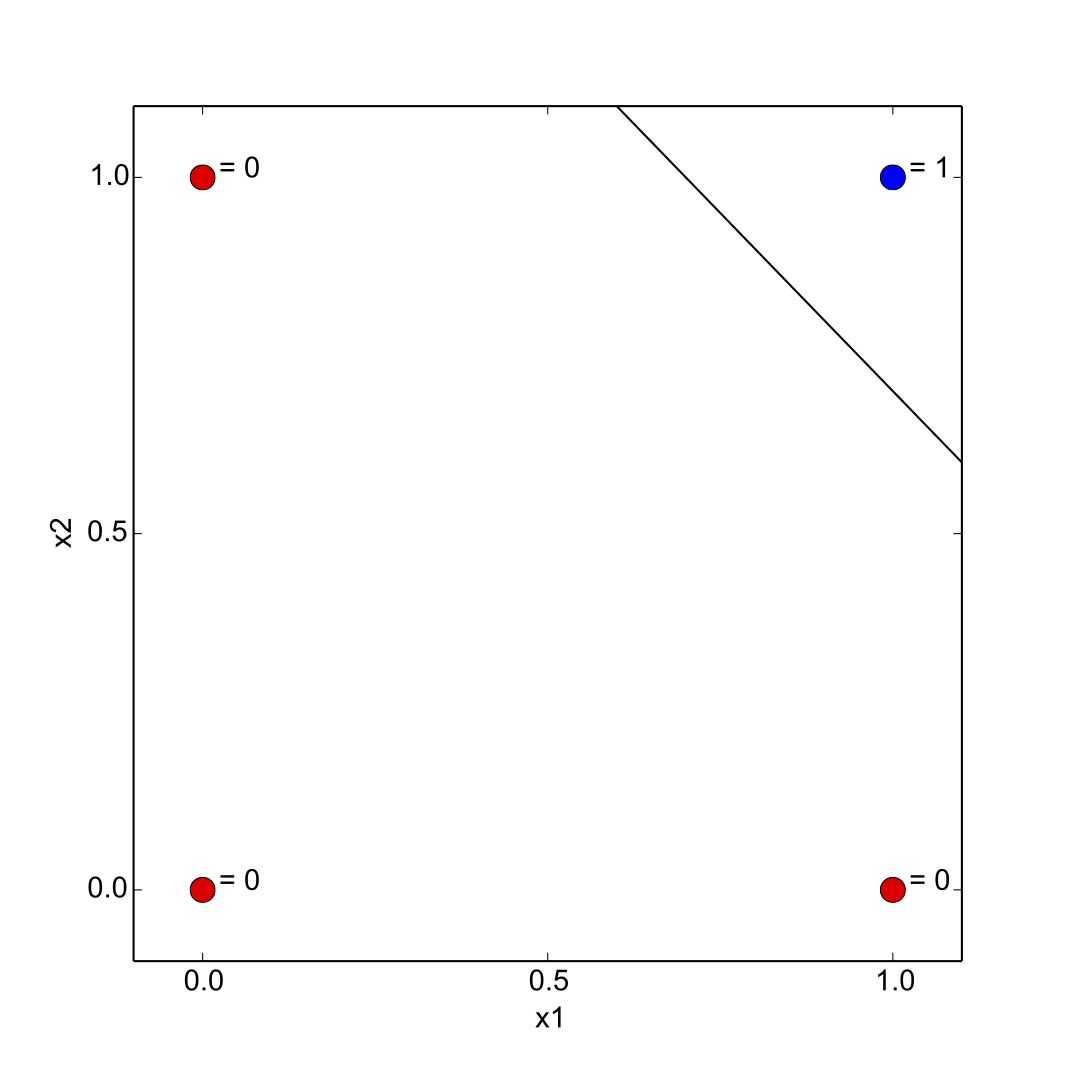
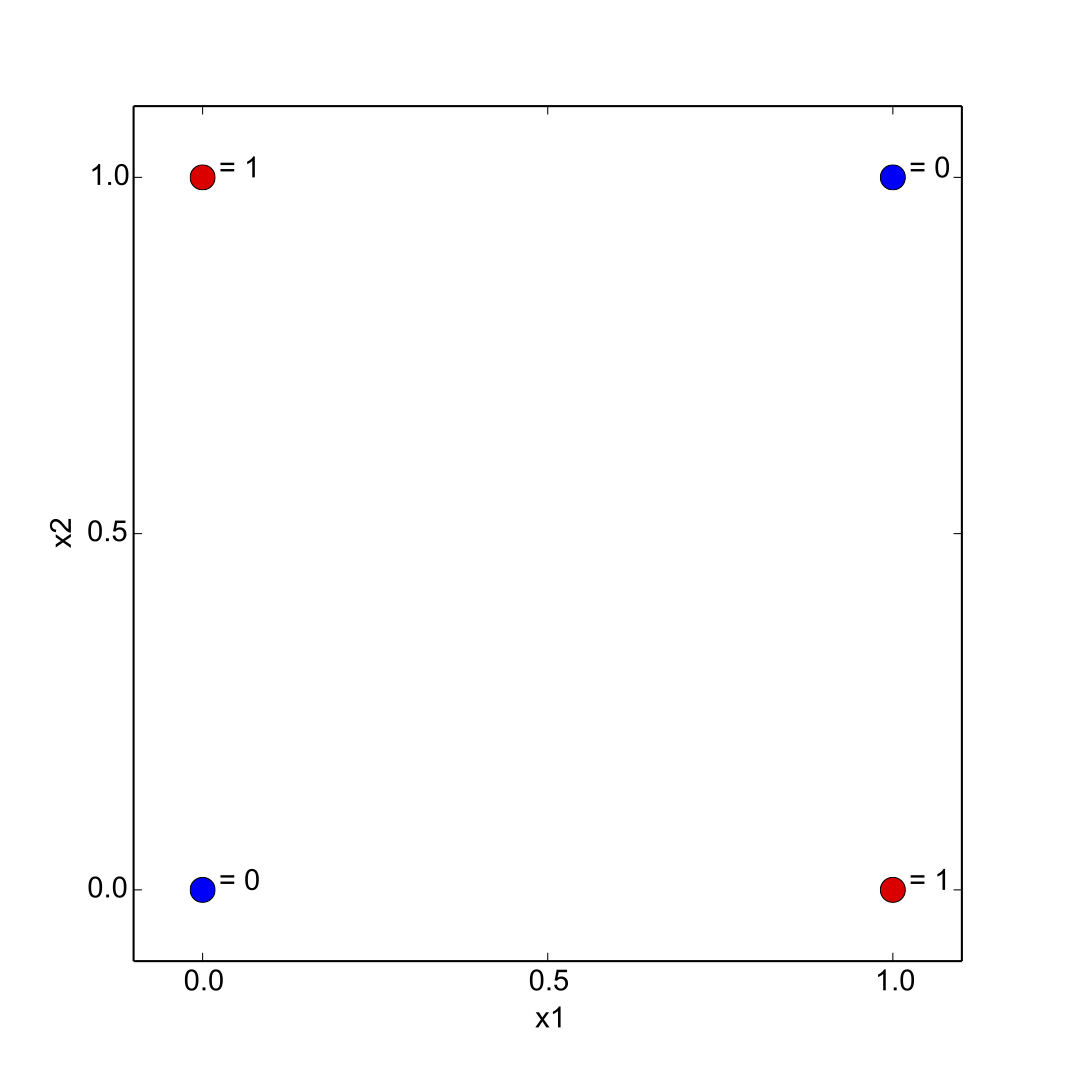
Perceptron si můžeme představit jako jakousi jednoduchou krabičku, která provádí vážený součet svých vstupů, ten pošle do aktivační funkce a aktivační funkce nám z krabičky vrátí výsledek. Na obrázku si to můžeme představit takto:
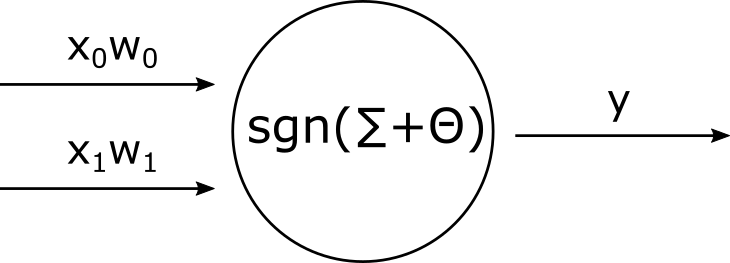
Do perceptronu vstupuje vektor $\widetilde{x}$ o dvou prvích: $x_0$, $x_1$. Hodnota každého vstupu je potlačena nebo zesílena váhou $w_n$. Perceptron provede součet všech těchto součinů a ten pošle do aktivační funkce - v našem případě to bude $\text{sgn}$. Pokud bude součet záporný, výsledek funkce je 0, jinak 1. Tuto funkci si nadefinujeme takto:
$$ \text{sgn}(x) = \begin{cases} 0, & x \leq 0 \\ 1, & x \gt 0 \end{cases} $$Odezvu celého perceptronu pak:
\begin{equation} y(t) = sgn\left(\sum_{i=0}^n w_i(t) x_i(t) - \Theta \right) \text{ .} \end{equation}$\Theta$ je tzv. bias, práh. K prahu budeme nahlížet jako k další, přidané váze. Jaký má přesný význam práh se pokusím vysvětlit v textu níže při vykreslování dělící přímky. Zatím bychom však rádi celou rovnici pro výpočet odezvy perceptronu zobecnili. V praxi se proto práh spojí napřímo se vstupem, který vždy bude mít hodnotu 1. Ve 2D prostoru budeme mít tedy 3 vstupní proměnné (2 s kterými budeme pracovat a jednu s pevnou hodnotou 1). Výsledný vzorec pak bude nabývat tvaru:
\begin{equation} y(t) = sgn\left(\sum_{i=0}^n w_i(t) x_i(t)\right) \text{ .} \end{equation}Pojďme se na celý proces výpočtu odezvy a učení podívat jako na celek a trošku více formálně:
- Váhy perceptronu $w_i(t)$ se inicializují náhodně malými čísly a $t$ je v tomto případě jednotka času, resp. iterace.
- Spustí se dopředný chod sítě a zjistí se hodnota $y(t)$: \begin{equation} y(t) = sgn\left(\sum_{i=0}^n w_i(t) x_i(t) \right) \text{ .} \end{equation}
- Adaptace vah na základě pravidla:
- výstup je správný: $w_i(t+1) = w_i(t) \text{ .}$
- výstup je 0 a měl být 1: $w_i(t+1) = w_i(t) + \eta x_i(t) \text{ .}$
- výstup je 1 a měl být 0: $w_i(t+1) = w_i(t) - \eta x_i(t) \text{ .}$
A teď zase trošku méně formálně a s příkladem.
Máme třídicí linku na léky. Linka je připojena k senzorům, které nám dávají na výstup barvu léku a jeho velikost. Barva je získaná jako číselná hodnota 0-360 (odstín v barevném modelu HSV) a velikost jako počet nasnímaných bodů na stínítku (snímací plocha bude mít 100x100 bodů). Našim úkolem bude vybrat pomocí linky pouze takové tablety, které mají modrou barvu a ideální velikost 25x25 bodů.
Ke klasifikaci léků využijeme perceptron. Ten bude léky klasifikovat do dvou tříd: 0, pokud se jedná o lék, který nevyhovuje stanoveným požadavkům a nás tedy nezajímá, nebo 1, za předpokladu, že lék vyhovuje daným požadavkům. Máme k dispozici trénovací/referenční sadu tablet, u kterých známe jejich parametry a třídu, do které patří. Aby se nám s daty dobře pracovalo, normalizujeme je - barvu vydělíme 360, čímž dostaneme hodnoty od 0 do 1. To samé uděláme s plochou. Jelikož známe celkovou plochu stínítka, plochu tablety vydělíme 10 000. Tato trénovací sada je dána následující tabulkou:
| Barva ($x_0$) | Plocha ($x_1$) | Třída ($z$) |
|---|---|---|
| 218 $\rightarrow$ 0.6 | 675 $\rightarrow$ 0.0675 | 1 |
| 10 $\rightarrow$ 0.03 | 1632 $\rightarrow$ 0.1632 | 0 |
| 233 $\rightarrow$ 0.65 | 483 $\rightarrow$ 0.0483 | 1 |
| 201 $\rightarrow$ 0.56 | 525 $\rightarrow$ 0.0525 | 1 |
| 69 $\rightarrow$ 0.19 | 1440 $\rightarrow$ 0.1440 | 0 |
| 106 $\rightarrow$ 0.26 | 3000 $\rightarrow$ 0.3 | 0 |
V praxi samozřejmě platí, že čím více trénovacích dat máme, tím lépe jsme schopni případnou neuronovou síť naučit. Při získání trénovací množiny bychom nejdřív měli nad množinou provést analýzu, zda neobsahuje nějaké odlehlé hodnoty, které vznikly chybou měření. V takovýchto jednoduchých případech postačí pouhá kontrola, zda dataset neobsahuje například u barvy čísla větší než 360, menší než 0, případně pohledem na graf hodnot v prostoru ověřit, zda se některý z bodů nenalézá v podezřelé poloze.
Před tím, než do perceptronu pustíme nové data, které budeme chtít klasifikovat, naučíme jej (nastavíme správné váhy) za pomocí trénovací množiny a Hebbova učícího pravidla. Učení bude probíhat v cyklech a v každém jednom kroku času $(t)$ zjistíme aktuální odezvu perceptronu $(z)$ a na základě jejich rozdílu upravíme hodnoty vah. V prvním kroku musíme inicializovat váhy náhodnými hodnotami. Při učení budeme pracovat s koeficientem učení $ \eta = 0.1$
Jelikož není nic lepšího, něž si daný problém odkrokovat, zvizualizovat a sledovat, co se při učení děje, připravil jsem tento jednoduchý embed. Embed je vložený ve stránce jako iframe, což nemusí být úplně ideální, proto si jej můžete otevřít ve vlastním okdně zde.
Když máme síť naučenou na trénovací množině, můžeme na vstup poslat vektor neznámých hodnot $\widetilde{x}$. Námi natrénovaný perceptron by měl na základě dělící přímky správně klasifikovat nové data to správné třídy.
A proč je důležité míti bias? Aktivační rovnici můžeme zapsat právě jako obecnou rovnici dělící přímky:
$$ 0 = w_0 x_0 + w_1 x_1 + w_2 x_2 $$Hodnota $x_2$ je napevno připojena ke vstupu s hodnotou 1. Zbyde nám proto ve třetím koeficientu proměnná $w_2$. Když si tuto rovnici převedeme na explicitní rovnici přímky, získáme:
$$ y = - \frac{w_0 x}{w_1} - \frac{w_2}{w_1} $$Hodnota váhy $w_2$ nám tedy určuje posunutí na ose $x$. Pokud bychom neměli žádný práh, resp. měli bychom jej nulový, síť by se nám sice učila v tom smyslu, že by upravovala směrnici dělící přímky, vždy by však protínala bod $[0, 0]$. V mnoha případech se takto definovaná síť přeci jen naučí, protože si jistě dokážeme představit, že i tato dělící přímka je schopna rozdělit velké množství trénovacích množin na dvě části. Na druhou stranu, stejně tak velké množství množin nebude schopna tak kvalitně rozdělit a naučí se podstatně hůř a pomaleji.