Vydáno:
Bézierova křivka bývá v počítačové grafice hlavní metodou modelování křivek. Využívá se v nástrojích pro 3D modelování, vektorové grafice, při tvorbě fontů apod. Její hlavní přednost spočívá v intuitivní úpravě, kdy pouhým přesunutím řídících bodů můžeme vymodelovat křivku takovou, jak potřebujeme. Na podobném principu funguje také Fergusonova křivka, která je v případě Fergusonovy kubiky zadána dvěma body a dvěma tečnými vektory. Bézierova a Fergusonova křivka jsou navzájem snadno převoditelné. V praxi je však vhodnější upravovat polohu bodů, než směr a velikost tečných vektorů.
Při modelování složitějších tvarů nevyužíváme často křivky vyššího stupně než třetího (čtyř řídících bodů) z důvodu horší manipulace a úpravy. Využíváme spíše Bézierův spline - rozdělení křivky na úseky maximálně stupně $n$. V případě Bézierovy kubiky můžeme tuto křivku rozšířit dalšími 3 body. Poslední bod prvního úseku křivky je i počátečním bodem druhého úseku křivky. Často také chceme, aby byl přechod jedné části křivky na druhou v tomto bodě plynulý. Hovoříme přitom o spojitosti. Můžeme vyžadovat buď geometrickou spojitost (shodná velikost směrnice v bodě) nebo parametrickou (shodné tečné vektory).
Rovnice Bézierovy křivky
\begin{equation}
P(t) = \sum^n_{i=0}B_{i,n}(t)P_i
\end{equation}
kde $B_{i,n}$ je Bernsteinův polynom stupně $n$:
\begin{equation}
B_{i,n}(t) = {n \choose i}t^i(1-t)^{n-1} = \frac{n!}{i!(n-i)!}t^i(1-t)^{n-i}
\end{equation}
Pro Béziérovu kubiku získáme tyto polynomy:
\begin{align*}
B_{0,3}(t) ={}& (1-t)^3\\
B_{1,3}(t) ={}& 3t(1-t)^2\\
B_{2,3}(t) ={}& 3t^2(1-t)\\
P_{3,3}(t) ={}& t^3\\
\end{align*}
Rovnici můžeme nahradit maticovým zápisem:
\begin{equation}
P(t) =
{\begin{bmatrix}
t^3 & t^2 & t & 1
\end{bmatrix}
}
{\begin{bmatrix}
-1 & 3 & -3 & 1\\
3 & -6& 3 & 0 \\
-3 & 3 & 0 & 0 \\
1 & 0 & 0 & 0 \\
\end{bmatrix}
}
{\begin{bmatrix}
P_0\\
P_1\\
P_2\\
P_3\\
\end{bmatrix}
}
\end{equation}
Výpočet
Mějme zadány 4 řídící body:
\begin{align*}
P_0(t) ={}& [0,0]\\
P_1(t) ={}& [2,5]\\
P_2(t) ={}& [4,-5]\\
P_3(t) ={}& [6,0]\\
\end{align*}
Dosazením těchto bodů do parametrické rovnice získáme předpisy pro jednotlivé souřadnice:
\begin{align*}
x(t) ={}& 6t(1-t)^2 +12t^2(1-t)+6t^3\\
y(t) ={}& 15t(1-t)^2+-15t^2(1-t)
\end{align*}
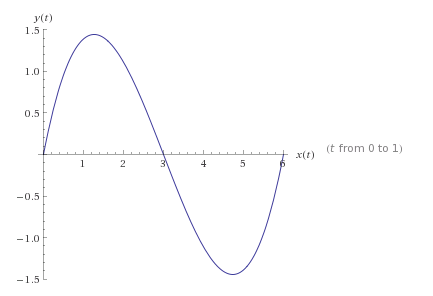
Výsledná křivka. Vykresleno pomocí Wolfram|Alpha
Vlastnosti Bézierovy křivky
- Křivka stupně $n$ je určena $n+1$ řídícími body
- Křivka pro parametr $t = 0$ začíná v počátečním řídícím bodě, pro parametr $t = 1$ končí v posledním řídícím bodě
- Tečný vektor v bodě $P_0$ je roven $n(P_1-P_0)$. Tečný vektor v bodě $P_n$ je roven $n(P_n-P_{n-1})$. Tohoto vztahu se dá využít při převodu na Fergusonovu křivku.
- Křivka se nachází uvnitř konvexního obalu tvořeného řídícími body